Functions for performing geographical position calculations using n-vectors
This library is a lightweight (<2kB), dependency-free port of the Matlab n-vector library by Kenneth Gade. All original functions are included, although the names of the functions and arguments have been changed in an attempt to clarify their purpose. In addition, this library includes some extra functions for vector and matrix operations needed to solve the 10 examples from the n-vector page.
See the reference documentation for a list of all functions and their signatures.
npm install nvector-geodesyThe following sections show the 10 examples from the n-vector page implemented using this library.
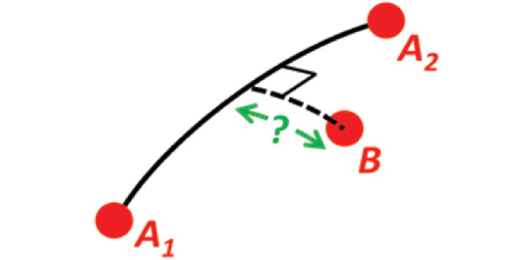
Given two positions A and B. Find the exact vector from A to B in meters north, east and down, and find the direction (azimuth/bearing) to B, relative to north. Use WGS-84 ellipsoid.
import {
delta,
fromGeodeticCoordinates,
radians,
toRotationMatrix,
transform,
transpose,
} from "nvector-geodesy";
import { expect, test } from "vitest";
/**
* Example 1: A and B to delta
*
* Given two positions A and B. Find the exact vector from A to B in meters
* north, east and down, and find the direction (azimuth/bearing) to B, relative
* to north. Use WGS-84 ellipsoid.
*
* @see https://www.ffi.no/en/research/n-vector/#example_1
*/
test("Example 1", () => {
// PROBLEM:
// Given two positions, A and B as latitudes, longitudes and depths (relative
// to Earth, E):
const aLat = 1,
aLon = 2,
aDepth = 3;
const bLat = 4,
bLon = 5,
bDepth = 6;
// Find the exact vector between the two positions, given in meters north,
// east, and down, and find the direction (azimuth) to B, relative to north.
//
// Details:
//
// - Assume WGS-84 ellipsoid. The given depths are from the ellipsoid surface.
// - Use position A to define north, east, and down directions. (Due to the
// curvature of Earth and different directions to the North Pole, the north,
// east, and down directions will change (relative to Earth) for different
// places. Position A must be outside the poles for the north and east
// directions to be defined.
// SOLUTION:
// Step 1
//
// First, the given latitudes and longitudes are converted to n-vectors:
const a = fromGeodeticCoordinates(radians(aLon), radians(aLat));
const b = fromGeodeticCoordinates(radians(bLon), radians(bLat));
// Step 2
//
// When the positions are given as n-vectors (and depths), it is easy to find
// the delta vector decomposed in E. No ellipsoid is specified when calling
// the function, thus WGS-84 (default) is used:
const abE = delta(a, b, aDepth, bDepth);
// Step 3
//
// We now have the delta vector from A to B, but the three coordinates of the
// vector are along the Earth coordinate frame E, while we need the
// coordinates to be north, east and down. To get this, we define a
// North-East-Down coordinate frame called N, and then we need the rotation
// matrix (direction cosine matrix) rEN to go between E and N. We have a
// simple function that calculates rEN from an n-vector, and we use this
// function (using the n-vector at position A):
const rEN = toRotationMatrix(a);
// Step 4
//
// Now the delta vector is easily decomposed in N. Since the vector is
// decomposed in E, we must use rNE (rNE is the transpose of rEN):
const abN = transform(transpose(rEN), abE);
// Step 5
//
// The three components of abN are the north, east and down displacements from
// A to B in meters. The azimuth is simply found from element 1 and 2 of the
// vector (the north and east components):
const azimuth = Math.atan2(abN[1], abN[0]);
expect(abN[0]).toBeCloseTo(331730.2347808944, 8);
expect(abN[1]).toBeCloseTo(332997.8749892695, 8);
expect(abN[2]).toBeCloseTo(17404.27136193635, 8);
expect(azimuth).toBeCloseTo(radians(45.10926323826139), 15);
});Given the position of vehicle B and a bearing and distance to an object C. Find the exact position of C. Use WGS-72 ellipsoid.
import {
WGS_72,
degrees,
destination,
eulerZYXToRotationMatrix,
multiply,
normalize,
radians,
toGeodeticCoordinates,
toRotationMatrix,
transform,
type Vector,
} from "nvector-geodesy";
import { expect, test } from "vitest";
/**
* Example 2: B and delta to C
*
* Given the position of vehicle B and a bearing and distance to an object C.
* Find the exact position of C. Use WGS-72 ellipsoid.
*
* @see https://www.ffi.no/en/research/n-vector/#example_2
*/
test("Example 2", () => {
// PROBLEM:
// A radar or sonar attached to a vehicle B (Body coordinate frame) measures
// the distance and direction to an object C. We assume that the distance and
// two angles measured by the sensor (typically bearing and elevation relative
// to B) are already converted (by converting from spherical to Cartesian
// coordinates) to the vector bcB (i.e. the vector from B to C, decomposed in
// B):
const bcB: Vector = [3000, 2000, 100];
// The position of B is given as an n-vector and a depth:
const b = normalize([1, 2, 3]);
const bDepth = -400;
// The orientation (attitude) of B is given as rNB, specified as yaw, pitch,
// roll:
const rNB = eulerZYXToRotationMatrix(radians(10), radians(20), radians(30));
// Use the WGS-72 ellipsoid:
const e = WGS_72;
// Find the exact position of object C as an n-vector and a depth.
// SOLUTION:
// Step 1
//
// The delta vector is given in B. It should be decomposed in E before using
// it, and thus we need rEB. This matrix is found from the matrices rEN and
// rNB, and we need to find rEN, as in Example 1:
const rEN = toRotationMatrix(b);
// Step 2
//
// Now, we can find rEB y using that the closest frames cancel when
// multiplying two rotation matrices (i.e. N is cancelled here):
const rEB = multiply(rEN, rNB);
// Step 3
//
// The delta vector is now decomposed in E:
const bcE = transform(rEB, bcB);
// Step 4
//
// It is now easy to find the position of C using destination (with custom
// ellipsoid overriding the default WGS-84):
const [c, cDepth] = destination(b, bcE, bDepth, e);
// Use human-friendly outputs:
const [lon, lat] = toGeodeticCoordinates(c);
const height = -cDepth;
expect(degrees(lat)).toBeCloseTo(53.32637826433107, 13);
expect(degrees(lon)).toBeCloseTo(63.46812343514746, 13);
expect(height).toBeCloseTo(406.0071960700098, 15);
});Given an ECEF-vector of a position. Find geodetic latitude, longitude and height (using WGS-84 ellipsoid).
import {
apply,
degrees,
fromECEF,
toGeodeticCoordinates,
type Vector,
} from "nvector-geodesy";
import { expect, test } from "vitest";
/**
* Example 3: ECEF-vector to geodetic latitude
*
* Given an ECEF-vector of a position. Find geodetic latitude, longitude and
* height (using WGS-84 ellipsoid).
*
* @see https://www.ffi.no/en/research/n-vector/#example_3
*/
test("Example 3", () => {
// PROBLEM:
// Position B is given as an “ECEF-vector” pb (i.e. a vector from E, the
// center of the Earth, to B, decomposed in E):
const pb: Vector = apply((n) => n * 6371e3, [0.71, -0.72, 0.1]);
// Find the geodetic latitude, longitude and height, assuming WGS-84
// ellipsoid.
// SOLUTION:
// Step 1
//
// We have a function that converts ECEF-vectors to n-vectors:
const [b, bDepth] = fromECEF(pb);
// Step 2
//
// Find latitude, longitude and height:
const [lon, lat] = toGeodeticCoordinates(b);
const height = -bDepth;
expect(degrees(lat)).toBeCloseTo(5.685075734513181, 14);
expect(degrees(lon)).toBeCloseTo(-45.40066325579215, 14);
expect(height).toBeCloseTo(95772.10761821801, 15);
});Given geodetic latitude, longitude and height. Find the ECEF-vector (using WGS-84 ellipsoid).
import { fromGeodeticCoordinates, radians, toECEF } from "nvector-geodesy";
import { expect, test } from "vitest";
/**
* Example 4: Geodetic latitude to ECEF-vector
*
* Given geodetic latitude, longitude and height. Find the ECEF-vector (using
* WGS-84 ellipsoid).
*
* @see https://www.ffi.no/en/research/n-vector/#example_4
*/
test("Example 4", () => {
// PROBLEM:
// Geodetic latitude, longitude and height are given for position B:
const bLat = 1;
const bLon = 2;
const bHeight = 3;
// Find the ECEF-vector for this position.
// SOLUTION:
// Step 1: First, the given latitude and longitude are converted to n-vector:
const b = fromGeodeticCoordinates(radians(bLon), radians(bLat));
// Step 2: Convert to an ECEF-vector:
const pb = toECEF(b, -bHeight);
expect(pb[0]).toBeCloseTo(6373290.277218279, 8);
expect(pb[1]).toBeCloseTo(222560.2006747365, 8);
expect(pb[2]).toBeCloseTo(110568.8271817859, 8);
});Given position A and B. Find the surface distance (i.e. great circle distance) and the Euclidean distance.
import {
apply,
cross,
dot,
fromGeodeticCoordinates,
norm,
radians,
} from "nvector-geodesy";
import { expect, test } from "vitest";
/**
* Example 5: Surface distance
*
* Given position A and B. Find the surface distance (i.e. great circle
* distance) and the Euclidean distance.
*
* @see https://www.ffi.no/en/research/n-vector/#example_5
*/
test("Example 5", () => {
// PROBLEM:
// Given two positions A and B as n-vectors:
const a = fromGeodeticCoordinates(radians(0), radians(88));
const b = fromGeodeticCoordinates(radians(-170), radians(89));
// Find the surface distance (i.e. great circle distance). The heights of A
// and B are not relevant (i.e. if they do not have zero height, we seek the
// distance between the points that are at the surface of the Earth, directly
// above/below A and B). The Euclidean distance (chord length) should also be
// found.
// Use Earth radius r:
const r = 6371e3;
// SOLUTION:
// Find the great circle distance:
const gcd = Math.atan2(norm(cross(a, b)), dot(a, b)) * r;
// Find the Euclidean distance:
const ed = norm(apply((b, a) => b - a, b, a)) * r;
expect(gcd).toBeCloseTo(332456.4441053448, 9);
expect(ed).toBeCloseTo(332418.7248568097, 9);
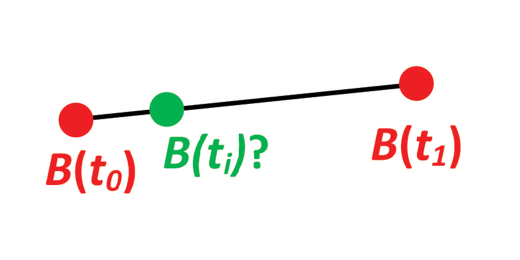
});Given the position of B at time t0 and t1. Find an interpolated position at time ti.
import {
apply,
degrees,
fromGeodeticCoordinates,
normalize,
radians,
toGeodeticCoordinates,
} from "nvector-geodesy";
import { expect, test } from "vitest";
/**
* Example 6: Interpolated position
*
* Given the position of B at time t(0) and t(1). Find an interpolated position
* at time t(i).
*
* @see https://www.ffi.no/en/research/n-vector/#example_6
*/
test("Example 6", () => {
// PROBLEM:
// Given the position of B at time t0 and t1, pt0 and pt1:
const t0 = 10,
t1 = 20,
ti = 16;
const pt0 = fromGeodeticCoordinates(radians(-150), radians(89.9));
const pt1 = fromGeodeticCoordinates(radians(150), radians(89.9));
// Find an interpolated position at time ti, pti. All positions are given as
// n-vectors.
// SOLUTION:
// Standard interpolation can be used directly with n-vectors:
const pti = normalize(
apply((pt0, pt1) => pt0 + ((ti - t0) * (pt1 - pt0)) / (t1 - t0), pt0, pt1),
);
// Use human-friendly outputs:
const [lon, lat] = toGeodeticCoordinates(pti);
expect(degrees(lat)).toBeCloseTo(89.91282199988446, 12);
expect(degrees(lon)).toBeCloseTo(173.4132244463705, 12);
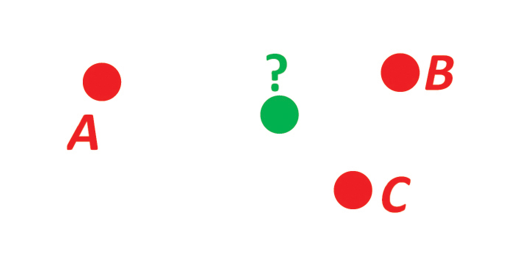
});Given three positions A, B, and C. Find the mean position (center/midpoint).
import {
apply,
fromGeodeticCoordinates,
normalize,
radians,
} from "nvector-geodesy";
import { expect, test } from "vitest";
/**
* Example 7: Mean position/center
*
* Given three positions A, B, and C. Find the mean position (center/midpoint).
*
* @see https://www.ffi.no/en/research/n-vector/#example_7
*/
test("Example 7", () => {
// PROBLEM:
// Three positions A, B, and C are given as n-vectors:
const a = fromGeodeticCoordinates(radians(0), radians(90));
const b = fromGeodeticCoordinates(radians(10), radians(60));
const c = fromGeodeticCoordinates(radians(-20), radians(50));
// Find the mean position, M. Note that the calculation is independent of the
// heights/depths of the positions.
// SOLUTION:
// The mean position is simply given by the mean n-vector:
const m = normalize(apply((a, b, c) => a + b + c, a, b, c));
expect(m[0]).toBeCloseTo(0.3841171702926, 16);
expect(m[1]).toBeCloseTo(-0.04660240548568945, 16);
expect(m[2]).toBeCloseTo(0.9221074857571395, 16);
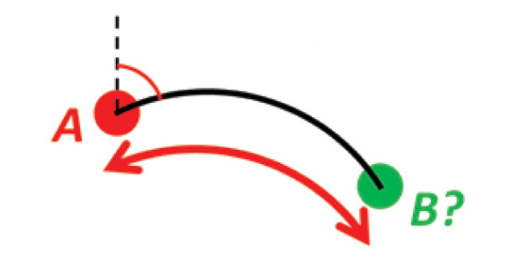
});Given position A and an azimuth/bearing and a (great circle) distance. Find the destination point B.
import {
Z_AXIS_NORTH,
apply,
cross,
degrees,
fromGeodeticCoordinates,
normalize,
radians,
toGeodeticCoordinates,
transform,
transpose,
} from "nvector-geodesy";
import { expect, test } from "vitest";
/**
* Example 8: A and azimuth/distance to B
*
* Given position A and an azimuth/bearing and a (great circle) distance. Find
* the destination point B.
*
* @see https://www.ffi.no/en/research/n-vector/#example_8
*/
test("Example 8", () => {
// PROBLEM:
// Position A is given as n-vector:
const a = fromGeodeticCoordinates(radians(-90), radians(80));
// We also have an initial direction of travel given as an azimuth (bearing)
// relative to north (clockwise), and finally the distance to travel along a
// great circle is given:
const azimuth = radians(200);
const gcd = 1000;
// Use Earth radius r:
const r = 6371e3;
// Find the destination point B.
//
// In geodesy, this is known as "The first geodetic problem" or "The direct
// geodetic problem" for a sphere, and we see that this is similar to Example
// 2, but now the delta is given as an azimuth and a great circle distance.
// "The second/inverse geodetic problem" for a sphere is already solved in
// Examples 1 and 5.
// SOLUTION:
// The azimuth (relative to north) is a singular quantity (undefined at the
// Poles), but from this angle we can find a (non-singular) quantity that is
// more convenient when working with vector algebra: a vector d that points in
// the initial direction. We find this from azimuth by first finding the north
// and east vectors at the start point, with unit lengths.
//
// Here we have assumed that our coordinate frame E has its z-axis along the
// rotational axis of the Earth, pointing towards the North Pole. Hence, this
// axis is given by [1, 0, 0]:
const e = normalize(cross(transform(transpose(Z_AXIS_NORTH), [1, 0, 0]), a));
const n = cross(a, e);
// The two vectors n and e are horizontal, orthogonal, and span the tangent
// plane at the initial position. A unit vector d in the direction of the
// azimuth is now given by:
const d = apply(
(n, e) => n * Math.cos(azimuth) + e * Math.sin(azimuth),
n,
e,
);
// With the initial direction given as d instead of azimuth, it is now quite
// simple to find b. We know that d and a are orthogonal, and they will span
// the plane where b will lie. Thus, we can use sin and cos in the same manner
// as above, with the angle traveled given by gcd / r:
const b = apply(
(a, d) => a * Math.cos(gcd / r) + d * Math.sin(gcd / r),
a,
d,
);
// Use human-friendly outputs:
const [lon, lat] = toGeodeticCoordinates(b);
expect(degrees(lat)).toBeCloseTo(79.99154867339445, 13);
expect(degrees(lon)).toBeCloseTo(-90.01769837291397, 13);
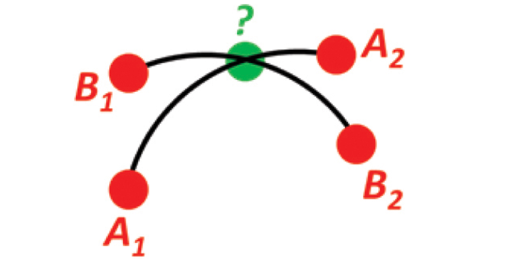
});Given path A going through A1 and A2, and path B going through B1 and B2. Find the intersection of the two paths.
import {
apply,
cross,
degrees,
dot,
fromGeodeticCoordinates,
normalize,
radians,
toGeodeticCoordinates,
} from "nvector-geodesy";
import { expect, test } from "vitest";
/**
* Example 9: Intersection of two paths
*
* Given path A going through A(1) and A(2), and path B going through B(1) and
* B(2). Find the intersection of the two paths.
*
* @see https://www.ffi.no/en/research/n-vector/#example_9
*/
test("Example 9", () => {
// PROBLEM:
// Define a path from two given positions (at the surface of a spherical
// Earth), as the great circle that goes through the two points (assuming that
// the two positions are not antipodal).
// Path A is given by a1 and a2:
const a1 = fromGeodeticCoordinates(radians(180), radians(50));
const a2 = fromGeodeticCoordinates(radians(180), radians(90));
// While path B is given by b1 and b2:
const b1 = fromGeodeticCoordinates(radians(160), radians(60));
const b2 = fromGeodeticCoordinates(radians(-140), radians(80));
// Find the position C where the two paths intersect.
// SOLUTION:
// A convenient way to represent a great circle is by its normal vector (i.e.
// the normal vector to the plane containing the great circle). This normal
// vector is simply found by taking the cross product of the two n-vectors
// defining the great circle (path). Having the normal vectors to both paths,
// the intersection is now simply found by taking the cross product of the two
// normal vectors:
const cTmp = normalize(cross(cross(a1, a2), cross(b1, b2)));
// Note that there will be two places where the great circles intersect, and
// thus two solutions are found. Selecting the solution that is closest to
// e.g. a1 can be achieved by selecting the solution that has a positive dot
// product with a1 (or the mean position from Example 7 could be used instead
// of a1):
const c = apply((n) => Math.sign(dot(cTmp, a1)) * n, cTmp);
// Use human-friendly outputs:
const [lon, lat] = toGeodeticCoordinates(c);
expect(degrees(lat)).toBeCloseTo(74.16344802135536, 16);
expect(degrees(lon)).toBeCloseTo(180, 16);
});Given path A going through A1 and A2, and a point B. Find the cross track distance/cross track error between B and the path.
import {
cross,
dot,
fromGeodeticCoordinates,
normalize,
radians,
} from "nvector-geodesy";
import { expect, test } from "vitest";
/**
* Example 10: Cross track distance (cross track error)
*
* Given path A going through A(1) and A(2), and a point B. Find the cross track
* distance/cross track error between B and the path.
*
* @see https://www.ffi.no/en/research/n-vector/#example_10
*/
test("Example 10", () => {
// PROBLEM:
// Path A is given by the two n-vectors a1 and a2 (as in the previous
// example):
const a1 = fromGeodeticCoordinates(radians(0), radians(0));
const a2 = fromGeodeticCoordinates(radians(0), radians(10));
// And a position B is given by b:
const b = fromGeodeticCoordinates(radians(0.1), radians(1));
// Find the cross track distance between the path A (i.e. the great circle
// through a1 and a2) and the position B (i.e. the shortest distance at the
// surface, between the great circle and B). Also, find the Euclidean distance
// between B and the plane defined by the great circle.
// Use Earth radius r:
const r = 6371e3;
// SOLUTION:
// First, find the normal to the great circle, with direction given by the
// right hand rule and the direction of travel:
const c = normalize(cross(a1, a2));
// Find the great circle cross track distance:
const gcd = -Math.asin(dot(c, b)) * r;
// Finding the Euclidean distance is even simpler, since it is the projection
// of b onto c, thus simply the dot product:
const ed = -dot(c, b) * r;
// For both gcd and ed, positive answers means that B is to the right of the
// track.
expect(gcd).toBeCloseTo(11117.79911014538, 9);
expect(ed).toBeCloseTo(11117.79346740667, 9);
});If you look at the test suite for this library, you'll see that there are very few concrete test cases. Instead, this library uses model-based testing, powered by fast-check, and using the Python nvector library as the "model", or reference implementation.
In other words, this library is tested by generating large amounts of "random" inputs, and then comparing the output with the Python library. This allowed me to quickly port the library with a high degree of confidence in its correctness, without a deep understanding of the underlying mathematics.
If you find any issues with the implementations, there's a good chance that the issue will also be present in the Python library, and an equally good chance that I won't personally understand how to fix it 😅 Still, don't let that stop you from opening an issue or a pull request!
- Gade, K. (2010). A Non-singular Horizontal Position Representation, The Journal of Navigation, Volume 63, Issue 03, pp 395-417, July 2010.
- The n-vector page
- Ellipsoid data taken from chrisveness/geodesy